[Estimated time: 5 mins]
Simpson’s paradox appears when a trend that appears in aggregated data disappears or reverses when the groups are separated. It was first discovered in 1951 by Edward Simpson, a statistician, when he noticed a drug that appeared to be bad for women and bad for men, but good for people overall. Such a drug cannot exist—it only appeared to because of how Simpson had analysed the data.
This post focuses on the more famous example of Simpson’s paradox, involving apparent gender discrimination at UC Berkeley. I’ve heard this case referred to multiple times before reading The Book of Why, but Judea Pearl gave a deeper and more interesting explanation than any I’d heard before.
The UC Berkeley case
In 1973, Eugene Hammel, an associate dean at UC Berkeley, noticed that their admission rates appeared to show a statistically significant bias against women, with 35% women admitted vs 44% men. So he got a statistician, Peter Bickel to have a closer look at this.
Bickel found that the lower rates of admission for women was because women tended to apply to more competitive faculties with lower admission rates (e.g. English). When broken down by faculty, the data actually showed a small but statistically significant bias in favour of women. Bickel and Hammel therefore concluded that UC Berkeley did not engage in discrimination because they couldn’t control which faculties people applied to. They published their results in a paper in Science in 1975.
Most explanations tend to stop there. No, there’s no discrimination against women, because the apparent bias disappears once you condition on faculty. But few people ask—should Bickel and Hammel have conditioned on faculty?
Should they have broken down the data by faculty?
The answer to this question depends on your theory of causation. Bickel and Hammel had implicitly assumed a causal diagram like this (they did not draw this though, and the picture comes from Judea Pearl instead):
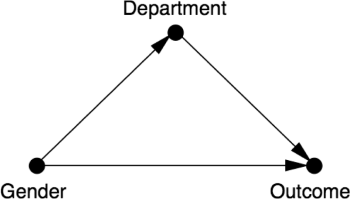
Here, Gender may causally affect both Department and Outcome. But Department also affects Outcome, so it acts as a mediator between Gender and Outcome.
When determining whether or not there has been discrimination, we are only interested in the direct path between Gender and Outcome. So, according to the above diagram, you should condition on Department to disable the indirect (back-door) path between Gender and Outcome. That will then give you the effect of the direct path only.
In other words, if the diagram above is accurate, Bickel and Hammel were absolutely right to break down the data by faculty.
But what if there’s a confounder?
William Kruskal, another esteemed statistician, wrote to Bickel and Hammel after reading their paper in Science. He argued that their explanation did not rule out discrimination, and queried whether any purely observational study (as opposed to an RCT with, say, fake application forms) could do so.
He suggested that there could be some other lurking confounder, such as State of Residence, that could affect both an applicant’s choice of Department and their Outcome. In other words, Kruskal implicitly suggested a diagram like this:
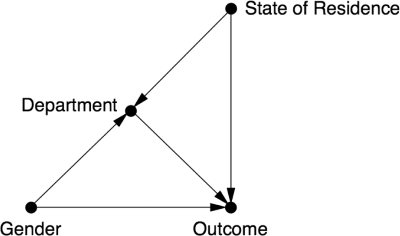
As with Bickel and Hammel, Kruskal didn’t use a causal diagram. Instead, he worked through a hypothetical example with two discriminatory departments that produced exactly the same data as Bickel’s did. In his example, both departments would accept all in-state males and out-of-state females and reject all out-of-state males and in-state females. This would be blatant discrimination, yet they would produce exactly the same numbers results as in Bickel’s example.
Bias is a slippery statistical notion, which may disappear if you slice the data a different way. Discrimination, as a causal concept, reflects reality and must remain stable.
Note that Kruskal wasn’t claiming that UC Berkeley was discriminatory. He was merely saying that Bickel and Hammel couldn’t rule it out from observational data. The problem with Bickel and Hammel’s argument was that it’s not clear which variables should be controlled for. If the State of Residence was a confounder, they would need to control for both Department and State of Residence. Since Department is a collider, conditioning on Department alone would open up the spurious indirect path: Gender → Department ← State of Residence → Outcome.
What’s the takeaway?
Nothing really ended up happening in the UC Berkeley case. But I nevertheless found this example illuminating because it shows how:
- there’s a limit to what causal conclusions you can draw from observational data;
- whether disaggregating data is the right move will depend on your understanding of the underlying causal relationships—which should be reflected in your causal diagram; and
- it’s hard to know if your causal diagram is correct because there’ll often be the possibility of unknown confounders.
Overall, this case highlights how important causal models are to guiding your statistical analysis.
If you enjoyed this explanation of Simpson’s Paradox, you may also like: