My latest summary is for The Art of Logic: How to Make Sense in a World that Doesn’t by Eugenia Cheng, which makes ideas from math and logic accessible by applying them to real world issues.
Estimated time: 28 mins
Buy The Art of Logic at: Amazon (affiliate link)
Key Takeaways from The Art of Logic
- Logic is a tool used to access mathematical truths, just like evidence is used to access scientific truths. While the real world is messier than the mathematical world, logic can still help you understand where a disagreement is coming from.
- Cheng explains some basic rules of logic and how they can apply to real life:
- Logical implications like “A implies B” let us make inferences about what is true.
- Logic has a directionality. “A implies B” may be true but the converse “B implies A” may not be.
- Negations. To negate a statement, you just show it is false. You don’t have to prove the opposite is true.
- Connectives. Words like “and” and “or” connect up statements to form more complex statements. The simple words can cause a lot of confusion.
- Logic tends to be binary. Logic doesn’t deal well with grey areas and can push us to extremes.
- Quantifiers. We can use quantifiers to refine the scope of our statements and be more correct.
- Abstraction and analogies are powerful ways to understand different situations better. There are different ways to abstract a situation—at higher levels of abstraction, you get broader principles but you lose some detail.
- All equations are actually lies. Apart from strict equalities (e.g. x = x), all equations are hiding something that is not true. Even 1 + 9 is not the same as 9 + 1. The answer may be the same but the process is different. A false equivalence is when someone equates two statements that are not actually the same in some crucial respect.
- Logic has limits.
- While logic lets us infer things from other things, our starting points or axioms are not rooted in logic. So two people with different axioms can be perfectly logical and still disagree.
- Logic can also run out of fuel if we don’t have enough information or time.
- Paradoxes can occur if we don’t set up our logic well.
- Emotions and logic can work together. We should use emotions to back up logic and logic to understand emotions.
- Sometimes people make emotional claims that are logically unsound. It’s usually more productive to look for the emotional truth in the claim instead of criticising the logic.
- Logic alone often won’t persuade people. Even in mathematics, if someone has an intuitive objection to your logical proof, they won’t use it or build on it.
- Being intelligent requires more than merely being logical. It requires being reasonable, being powerfully rational, and helpful.
Detailed Summary of The Art of Logic
What is logic?
Logic is a tool used to access mathematical truths. It sets out clear rules so that different people can consistently and unambiguously reach the same conclusions about whether something is true or false.
Many people think mathematics is just the study of numbers, but it’s more than that—it’s the logical study of how logical things work. Mathematical truths tend to be more robust than scientific truths because when logic tells us something is true, it’s true by logical implication—something inherent that will never change. A logical implication is true whether or not a human ever notices it.
Logic is to mathematics as evidence is to science.
Logical implications are much more powerful than pieces of evidence. A logical implication means something is definitely true, while a piece of evidence only contributes to the likelihood that something is true. This means mathematicians can reach agreement on what is true, and they tend to remain true for thousands of years.
Applying logic to real life
Since mathematics uses logic, it can only study objects that behave according to the rules of logic. But few things in life are as clean as mathematical proofs, so logical people can still disagree about real-life issues. Still, logic can help you understand where a disagreement is coming from and avoid some of it.
Throughout the book, Cheng employs a distinction between pedantry and precision. The difference between the two is illumination. Getting definitions and assumptions clear in order to construct logical arguments with them can be illuminating, because many arguments in real life go wrong when two people use different definitions or assumptions and just talk past each other. But when the extra precision doesn’t help, it’s mere pedantry—precision that has gone further than necessary to shed light on a situation.
Some basic rules of logic
Logical implications and inferences
A logical implication describes a relationship that is true, such as “If A then B” or “A implies B”. Note that “If … then …” and “implies” have special meanings in maths. In normal usage, they may describe a whole host of different relationships that may just be probabilistic or speculative. But in logic, the words are statements of logical implication.
The closer to a pure logical implication we get, the more obvious it should sound. For example: “If you are white then you have white privilege” is a more debatable statement than “If you are white in a place that has white privilege then you have white privilege.” Making a logical implication explicit can nevertheless give us new insights.
The process of concluding something from a logical implication is called inference. So if we know “A implies B”, then we can infer B from A:
1. A is true.
2. A implies B (or “A ⇒ B” in mathematical notation)
3. Therefore B is true.
The conclusion in #3 can be false if either of the first two statements are false.
This process of inference is fundamental to the use of logic, as it’s basically the only way we can progress from one known truth to another one. Logical proofs in mathematics work by chaining together a series of logical implications (e.g. A ⇒ B; B ⇒ C; C ⇒ D) . This lets us discover something new and perhaps surprising (A ⇒ D).
The directionality of logic
Logic has a direction. The implication symbol ⇒ makes this clear.
If you turn the arrow around, you get a statement that is the converse of the original statement. The converse of “A ⇒ B” is “B ⇒ A”.
Example: Converse statements for broccoli and ice cream
A parent tells their child, “If you eat your broccoli you can have ice cream” (broccoli ⇒ ice cream). They’re saying that eating broccoli will be sufficient for earning ice cream.
But this statement doesn’t tell us whether the converse is true—is eating broccoli the only way to obtain ice cream? If the parent wants to convey that, they should say, “You get ice cream only if you eat broccoli” (ice cream ⇒ broccoli).
You make a converse error if you mistakenly assume that the converse of a statement is equivalent to the statement. The converse is logically independent of the first statement, meaning there is no logical connection between the two. It could be true—in which case A and B are logically equivalent (A ⇔ B) —or it could not.
Negations
In logic, we argue against things by negating them. This just means showing that the statement is untrue; we don’t have to prove the opposite is true.
Example: Negating a statement about the EU
Statement: The EU is fantastic.
Opposite: The EU is terrible.
Negation: The EU is not fantastic.
The negation is generally a broader statement than the opposite. It is possible to be “not fantastic” without being “terrible”.
If a statement is true, its negation must be false. If something is false, its negation must be true.
Connectives
The words “and” and “or” are connectives—they connect up different logical statements to form bigger, more complex statements. In ordinary conversation, connectives can be implied—e.g. if someone is a “white man”, they are white and a man.
Despite being very simple, these words can cause tons of logical mistakes. One example is with the word “or”.
The ambiguous “or”
The word “or” is tricky because it is used differently in maths than in normal life, which makes it logically ambiguous.
The inclusive “or” joins two statements “A” and “B” together to make a new statement, “A or B”. The statement is true if either A or B is true. This is the “or” typically used in maths. So if someone asks, “Would you like tea or coffee?” and you want tea, the correct answer in maths is “yes”, not “tea”.
The exclusive “or” excludes the possibility of both options. So if someone offers you tea or coffee, you have to pick one. This is much more common in everyday language. It’s usually clear from the context but you can emphasise it by adding the word “either” (“Would you like either tea or coffee?”).
Negating statements joined by connectives
To negate a statement joined by “and”, you only need to negate one of the two claims. For example, if you’re not a “white man”, you could be a non-white man, a white woman, or a non-white woman.
But to negate a statement joined by the inclusive “or”, you must negate both claims.
Causation, blame and responsibility
Everything in the real world is caused by a combination of factors. Changing any one of them could change the outcome. Or, in logical terms, to make the statement “A and B and C and D” false, you can negate any one of A, B, C or D.
Blame and responsibility are at the heart of many relationship breakdowns. Instead of trying to attribute blame individually, it’s often more productive to understand how factors interact with each other to cause an outcome. A person can take responsibility for changing an undesirable outcome even if they aren’t to blame for it. [See Difficult Conversations for a better explanation of the difference between blame and contribution.]
Outcomes are always caused by whole systems, but we can still as individuals take responsibility for change.
Factors can interact in ways that create vicious cycles. It’s important to understand when something is a cycle because it means that instead of looking for a single “root cause”, we can look to which factor is easiest to change.
Logic tends to be binary
In logic, the Law of the Excluded Middle says that every proposition is either true or not true. So on a sliding scale between black and white, you need to draw a line somewhere and classify everything as “black” or “not black”:

Alternatively, you can draw a line at the other end and classify everything as “white” or “not white”:

Neither approach is very satisfactory, because both push the dividing line to the extreme. But they’re at least more logically sound than drawing two lines at the extremes and “losing” the middle altogether:

Dealing with grey areas in real life
Life involves many grey areas. We should understand them for what they are, instead of ignoring them or forcing them to be black or white. Otherwise, logic can push us into extreme positions.
Example: It’s not logical to stop eating cake
Mathematical induction proceeds by small incremental steps. If you know something is true for the number 1, and if you have a way of climbing up by 1, then you know it’s true for all whole numbers.
For example:
- It’s okay to eat one small piece of cake; and
- Since it was fine to eat one small piece of cake, it’s okay to eat another.
Being strictly logical is not helpful in this situation. Logic pushes you to either eating no cake or infinite cake. Any dividing line between a sensible amount of cake and “too much” will be an arbitrary line in the grey area.
Two solutions include:
- Fuzzy logic. This is a type of formal logic that takes truth values in a range between 0 and 1. It measures the extent to which something is true. In the cake example, you might have gradations between the two extremes like “less fine”, “sort of okay but not great”, “dubious”, “a bit too much”, etc.
- Intermediate value theorem. Acknowledge that the line is somewhere in the grey and put bounds in a place you’re comfortable with. Where you put the line depends on how dire the consequences of getting it wrong are. For example, you may want to create a large buffer zone for sexual harassment by drawing the boundary somewhere before things even start being questionable.
Quantifiers
Mathematics uses the quantifiers “for all” and “there exists” to restrict the scope of our statements. These two go hand in hand:
- To negate a “for all” statement (e.g. “All female science students have been hit on by their supervisor”) you only need to show that “there exists” one such student who hasn’t. Sweeping statements like this are easy to negate.
- To negate a “there exists” statement (e.g. “There exists a female science student who has been hit on by their supervisor”) you need to show that “all” such students haven’t been hit on.
In real life, you can refine the scope of your statements to be more correct by using using qualifiers like:
- Quantity: almost all, most, some
- Subjectivity: in my opinion, in my experience
- Probability: maybe, probably, might
Abstraction
The real world is complex. To understand it logically, we have to simplify it by removing some details. This is abstraction.
Benefits of abstraction and analogies
Abstraction is powerful because many different situations become the same once you remove some details.
It can also help you find analogies, which are helpful in:
- Discovering axioms (see the example below about false negatives vs false positives).
- Testing principles. Things in the abstract world exist as soon as you think of them. You can then play with ideas using thought experiments and follow through the logical implications.
- Engaging emotions. Finding an analogous situation that resonates more closely with someone can establish an emotional connection to back up the logic. The example doesn’t justify the principle, but helps us feel it.
- Pointing out extremes. An extreme analogy can show that two opposing positions may just come down to differences in where to draw the line in a grey area. This can help bridge disagreements.
Of course, you can make analogies between two things without going up to the abstract level. But it’s easier to make more complicated analogies or find examples that are much further away from where you started if you make the abstract version explicit.
Example: False positives and false negatives
People disagree over the level of social services we have. This disagreement can be simplified to one over false positives vs false negatives:
- False positive is someone who doesn’t deserve help but gets it.
- False negative is someone who deserves help but doesn’t get it.
Whether you care more about false positives or negatives may determine whether you support expanding or reducing social services. But whether you care more about one or the other is not founded on logic (it’s alogical), so even if two people are being logical, someone who cares more about false negatives may simply never reach agreement with a person who cares more about false positives.
Abstracting the disagreement this way may also help you make connections with other arguments. Similar preferences may be at play in whether you believe you’re more likely to regret doing something you shouldn’t have (false positive) or not doing something you should have (false negative).
One of Cheng’s axioms is caring about false negatives more than false positives. Discovering this helped her clarify her thinking about various issues, ranging from affirmative action to sexual harassment to cancer screening, and better explain her positions more clearly to others. Finding this axiom also led her to change her mind about the merits of compulsory voting (the false negatives being people who are unable to vote for logistical or voter suppression reasons and the false positives being people who don’t want to vote but are forced to).
[I disagree with Cheng’s framing of this issue, for reasons explained here.]
How abstraction works
When you abstract, you go up a level to find the similarities between a general or abstract class. For example:
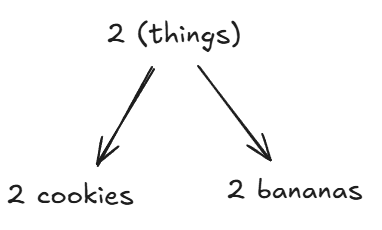
The process of abstraction is not itself logical. We choose what to focus on and what details to remove. A single situation may have many different abstractions that show us different things.
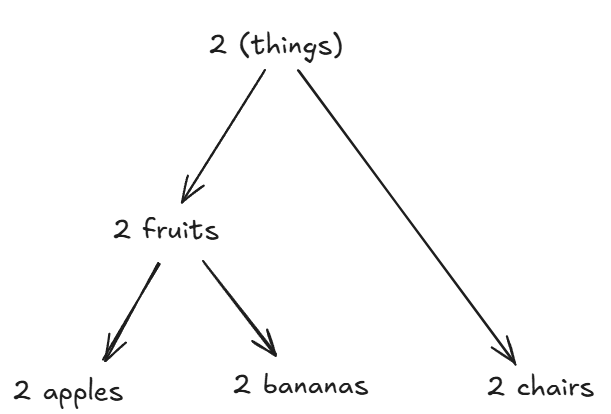
The more details we remove, the more things become the same. When we move up levels of abstraction, we get further away from the concrete ideas (vertically from “fruits” to “things” in the picture) but can pivot further and cover a broader range of ideas (horizontally from “things” to “chairs”). But if we go too far and remove critical or inherent details, we’re oversimplifying.
Logic and abstraction are like shining a light at things. As we get more abstract, it’s like raising the light off the ground. We see a broader context, but with less fierce detail; however, understanding the broad context helps us understand the detail later. In all cases the aim should be illumination of some kind.
When abstracting, we only remove details temporarily to understand the broader principle before putting those details back in. We should also remember what details we’ve removed so that we understand the limitations of abstraction.
Risks with abstraction
People can get into heated arguments when they pick the level of abstraction that suits their argument without considering that there can be other equally valid levels. Analogies can create problems when we do not make our abstract principles explicit and can lead to worse arguments.
Example: Abstraction and arguments around gay marriage
An argument comparing homosexuality to incest, paedophilia or bestiality can engage emotions in an unhelpful way. The analogies can be abstracted as follows:
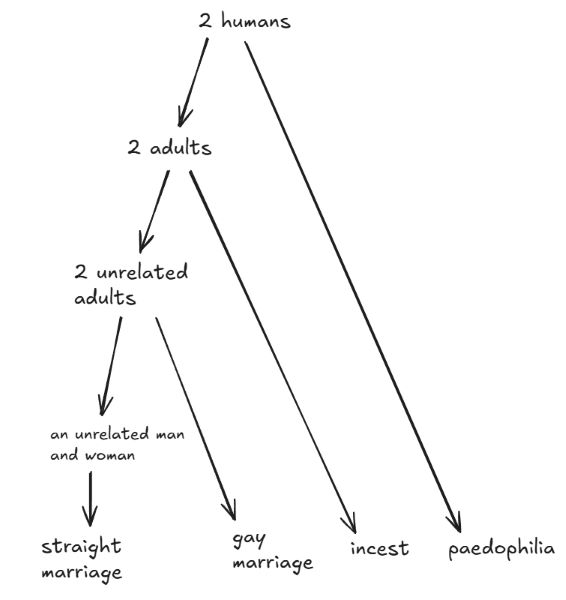
As we get more abstract, the examples become more extreme. But you can support gay marriage without going up to higher levels of abstraction. (We don’t have to eat infinite cake.)
It’s also worth remembering that there used to be levels below “an unrelated man and woman” as interracial marriages used to be illegal.
Cheng suggests the most reasonable abstract principle to infer from an analogy is the minimal one, like the lowest common multiple. But there is no right answer to what the “right” level of abstraction is because all analogies break down somewhere. The best we can do is understand the ways in which some situations are the same and the ways in which they are not.
All equations are actually lies
A common myth about mathematics is that it’s all about numbers and equations. But as maths progresses, it starts to involve things like shapes, curves, patterns and analogies. There are many ways in which these things can be the same (equivalent) or not the same as each other:
- Two triangles are congruent if they are exactly the same shape and size, and are similar if they have the same angles but different side lengths.
- Whether flipping a triangle over makes it a different shape depends on what you use it for.
- A square can be considered mostly the same as a circle when baking a cake, but not when making a wheel.
Example: 10 + 1 = 1 + 10 is not completely true
If you ask young children what 10 + 1 is, they will put 10 in their head, easily add 1 with their fingers, and get to 11. Yet if you ask them what 1 + 10 is, they will put 1 in their head, and arduously count to 10 with their fingers.
To them, 10 + 1 does not involve the same process as 1 + 10. In fact, in high-level mathematics, 1 + 10 is not defined to be the same thing as 10 + 1, either.
But the equation 10 + 1 = 1 + 10 is illuminating because it tells us that although both sides of the equation involve a different process, they will produce the same answer. So if you only care about the answer, you can pick whichever process is easiest. Virtually all equations in mathematics are like this.
Apart from strict equalities like x = x (which are not illuminating), all equations hide something is not an equality. And since things in life have multiple dimensions, we should be careful about claims that two things are the same.
False equivalence
Sometimes people use false equivalence as an attack tactic, by claiming that a statement is equivalent to a much worse one. One example is straw-man arguments, which replace an argument with the weaker “straw man” that is easier to knock down. Other times, people unconsciously equate a harmless statement with a more objectionable one, and then take offence.
Another example of false equivalence is a false dichotomy—when you mistakenly assume the only options are A and B. This can lead to the logical error “A = not B” or “B = not A” when in reality it may be possible to be both A and B or neither A nor B.
Claims of false equivalence must themselves be justified. When someone uses an analogy, they’re not claiming that two things are exactly the same since, as noted above, all analogies break down somewhere. The question is whether the two are equivalent in a crucial or irrelevant sense.
Limits of logic
We can’t rely on logic alone because it has limits. But that doesn’t mean we should throw it out, either. We should simply understand what those limits are and where we have to use emotions.
Sometimes we’ll have to be alogical, which is not the same as being illogical. We shouldn’t contradict logic—but we can’t be fully governed by it.
Where logic starts
Logic lets us deduce things from other things. It has to start somewhere, but the starting point cannot itself come from logic. For example, we might know “X implies Y”, but how do we know if X is true? Perhaps it’s because we know “W implies X”. But then how do we know if W is true?
This process of working backwards is how we build up logical arguments. But there’s no ultimate “starting point” in logic. At some point we just have to accept some assumptions or beliefs—at least for now—as the basis for your logical system without justifying them. In logic, these starting points are called axioms.
Axioms are the basic rules of the system. If you’re a logical person, everything you believe should follow from your axioms using logic, and those beliefs should not cause contradictions.
Importantly, two perfectly logical people can reach different conclusions if they start from different axioms. A belief is only illogical if it causes contradictions within a person’s belief system.
Axiomatising a system
Axiomatising a system means trying to find the basic truths that logically generate everything else that is true. A good set of axioms should be true, and also basic. Ideally you want as few axioms as possible, meaning you can’t break your axioms down into smaller parts. A famous example is Euclid’s axiomatisation of geometry with 5 rules.
Cheng has tried to axiomatise her own belief system by thinking about all the things she believes to be true, looking for the basic beliefs underlying them and trying to avoid logical contradictions. This process has helped her understand her own thinking and get to the root of disagreements faster. There are also cases where Cheng has noticed a contradiction that made her change her mind on an issue.
Whether a belief is a fundamental axiom or not is a grey area. If you take all beliefs as axioms, there’s no role for logical deduction or justification at all. This isn’t illogical per se, as it doesn’t contradict logic. It’s just not a very well-developed system of beliefs that will help you reach new insights.
Where logic ends
A logical proof in maths is sort of a like a tree. The “base” is what you’re trying to prove, and then you show the two (or more) key branches that make the base true, and then the branches that make those key branches true, and so on.
Strictly logical proofs are usually impractical to write down in full. Instead, you just sketch out the broad strokes first and then fill in the details. But at some point you have to stop filling in gaps. Like a machine running out of fuel, logic typically runs out of information. Life is complicated and much of it is unknowable, so we can’t rely solely on logic for our decisions. For example, we can never have full information about how another human being will act, so questions of trust cannot rely on logic alone.
Alternatively, you might run out of time, because logic is slow and feelings are faster.
Paradoxes exist
Paradoxes can occur when logic contradicts itself. To avoid this, we may need to take more care in setting up our logic, definitions, or scope.
Bertrand Russell’s Barber Paradox
Imagine a male barber in a town. The barber shaves all the men in the town who do not shave themselves, and nobody else. Who shaves the barber?
The problem is with the statement we started with—it’s impossible for such a barber to exist. This paradox warns us that, when defining a mathematical set, some descriptions allow sets that will result in a contradiction, so we have to exclude those.
Paradoxes may seem technical and abstract. However, this Barber Paradox helped Cheng think about what “tolerance” means. In her view, being tolerant doesn’t mean tolerating all views as that would mean you’d have to tolerate intolerant views. Rather, she refines the scope by adding some qualification—e.g. tolerating all views that do not hurt other people (or something like that)—which resolves the paradox that would otherwise occur.
Emotions
Emotions and logic are not diametrically opposed. You can be emotional and logical at the same time. We shouldn’t deny or suppress our emotions; we should use them.
Several ways emotions can help us include:
- Working out what we really believe in. Cheng respects and trusts her emotions, but always looks for logical explanations behind them.
- Generating new ideas. Emotions can help you think about what might be true before we start trying to logically prove it.
- Persuading other people. See above. People are rarely completely logical.
In this way, emotions should reinforce rather than supersede logic.
Look for the logic behind emotional claims
Feelings are facts in that they are always true. What someone ends up saying in an emotional outburst may not be true, but the feelings behind that outburst are true (as in, they exist). So it’s rarely useful to try to persuade someone that they “should not” feel something. Sometimes people can’t articulate the logic behind their feelings, but they aren’t necessarily being illogical.
Example: “Men are sexist pigs!”
When someone exclaims, “Men are sexist pigs!”, they probably don’t mean all men and maybe not even most.
What they really mean is probably, “I have encountered enough men who were sexist pigs today that I am fed up with it.” They’ve expressed true emotions with incorrect logic.
Some people will be tempted respond by arguing with the logic instead of addressing the emotions. However, looking for the emotional truth in someone’s statements can be much more productive than demonstrating they were logically wrong. This is an example of the principle of charity.
A more productive approach is try and understand the logic behind someone’s feelings. It’s like when student gives a wrong answer in a maths class—you should try to uncover the thought process behind their answer, instead of just giving them the right answer.
Once you understand someone’s feelings, you might then use emotions to bridge the gap between the other person’s logic and yours. Analogies are powerful in this regard, as they let you pivot from a situation where someone doesn’t feel anything to another situation where they have strong feelings.
Persuading people
You can’t use logic to persuade someone who isn’t convinced by logic. In this way, emotions can be more powerful than logic.
Even in maths, logic alone often fails to convince other people. Research papers will commonly include a more informal description that invokes ideas and imagery to help others understand the logical proof. The peer review process for getting mathematical proofs published also be a bit like trial by jury, where emotions and an author’s reputation can sway things. (Anonymous peer review doesn’t work because high-level mathematics is so specialised and researchers will often present early versions of their work at conferences to road-test it.)
Plus, readers can remain sceptical if the outcome doesn’t match their intuition even if the logic is sound. In theory, intuitive objections shouldn’t matter but in practice, they do. If other people aren’t convinced of your result, they won’t use it, build on it, or value it. They might follow every step of the logic but still feel disconcerted if they don’t feel it is true. So when someone has an intuitive objection to one of Cheng’s proofs, she’ll try to find the root of it and resolve it.
Intelligence involves more than merely being logical
Being intelligent requires more than just being logical. Intelligence also requires using logic in a way that seeks to help other people, which involves a mix of logical techniques and emotions.
Cheng suggests there are 3 more things you have to be to be “intelligent”:
- Reasonable or rational. This means accepting grey areas instead of going to extremes and having reasonable axioms. What counts as “reasonable” axiom is itself grey, but it should being open to changing your mind and having some framework to adjust your beliefs if you get new evidence.
- Powerfully rational. This involves using logic to build complex arguments and gain new insights. Someone who is powerfully rational can use the skills discussed above like abstraction, long chains of deduction, and separating out logic and emotions.
- Helpful. This means helping the world in some way, such as by bridging divides and fostering a more nuanced dialogue.
Other Interesting Points
- Note that I’ve left out many interesting math examples that are not core to the book but would take a lot of space to explain. One that I really liked gave a taste of category theory (Cheng’s specialty) by using prime factors and abstraction. I’ve also significantly cut down the section on “paradoxes”. I’d encourage you to check out the book if you like this stuff.
- In mathematics, the word “theory” describes a set of results that has been proved according to logic. There is no probability involved, no evidence required, and no doubt.
- A single proof in maths may take years to construct and only a few pages to write out. Cheng’s been working on one for 11 years, which has over 200 pages in notes.
My Review of The Art of Logic
Overall, I really liked The Art of Logic. I admit I did not like many of the examples chosen and her Cheng’s occasionally self-righteous tone, which I think explain the book’s rather dismal 3.47 Goodreads rating (lower than Twilight!). I’ve addressed these in my criticisms of The Art of Logic.
But if you can put those issues aside, The Art of Logic is well worth a read. There’s tons of great stuff in there from the explanations of abstraction to the limits of logic and the role of emotions. I also found it interesting to learn about a little about how higher-level maths and logical proofs work. Perhaps my favourite was the part about axiomatising your belief system since I’ve actually been working on something similar (kind of like Ray Dalio’s list of Principles, but more “basic”). Even when the book covered things I already knew, I found Cheng’s explanations helpful.
The book’s structure is also solid (as you might expect from a logician!) and the explanations are clear and accessible. You certainly don’t need a strong maths background to enjoy it. And, if you have an aversion to maths, hopefully The Art of Logic will give you a better appreciation for it.
Let me know what you think of my summary of The Art of Logic in the comments below!
Buy The Art of Logic at: Amazon <– This is an affiliate link, which means I may earn a small commission if you make a purchase through it. Thanks for supporting the site! 🙂
If you enjoyed this summary of The Art of Logic, you may also like:
- Book Summary: Algorithms to Live By by Brian Christian and Tom Griffiths. This book is similar to The Art of Logic as it makes ideas from computer science accessible by applying them to everyday situations (without the controversial examples).
- Book Summary: Calling Bullshit by Carl Bergstrom and Jevin West
- Book Summary: The Scout Mindset by Julia Galef
