[Estimated time: 3 mins]
The Monty Hall problem is a famous probability puzzle based on the game show Let’s Make a Deal. Here’s the setup: You’re presented with three closed doors. Behind one door is a car (the prize) and behind the other two are goats. You pick a door, say Door 1.
The host, Monty Hall, then opens one of the other doors to reveal a goat. You know from watching the show that he knows what’s behind each door and will always reveals a goat. Monty then asks if you’d like to stick with your original choice or switch to the remaining unopened door.
What should you do?

The solution says that you’re always better off switching your choice after the host has opened a door, because it will double your chances of winning from 1/3 to 2/3. If you find this counterintuitive—don’t worry, you’re not alone. I certainly struggled to understand it when I first encountered it. Even brilliant mathematicians like Paul Paul Erdős couldn’t believe it until someone proved it to him with a computer simulation.
Why You’re Better Off Switching
The key insight is that the door Monty opens is not random—it will never have the prize behind it.
As Judea Pearl explains in The Book of Why, the door you didn’t pick and which Monty didn’t open was vulnerable to refutation (i.e., Monty could have opened it), whereas the door you picked was not. Therefore, the door you didn’t pick becomes a more likely location for the prize, while the probability for your initial choice remains unchanged.
Let’s break down the possibilities if you pick Door 1:
- If the prize is behind Door 1: Monty can open either Door 2 or 3 (they both have goats). Switching would lose you the prize.
- If the prize is behind Door 2: Monty must open Door 3. Switching would win you the prize.
- If the prize is behind Door 3: Monty must open Door 2. Switching would win you the prize.
In two out of three scenarios, switching leads to victory. This is why switching doubles your odds from 1/3 to 2/3.
Important!
Switching is only beneficial if Monty knows where the prize is and never opens a door with the prize behind it. This was indeed the setup behind the show Let’s Make a Deal.
If this isn’t true—for instance, if Monty opens doors randomly—then switching offers no advantage.
Why is this so unintuitive?
Judea Pearl explains that we struggle with this problem because humans naturally think in causal terms, not probabilistic ones.
Here, we have correlation without (apparent) causation: when Monty opens a door, this correlates with the prize being more likely to be behind the remaining unopened door, and not your original choice. This correlation is confusing because there doesn’t seem to be any causality—Monty opening a door cannot cause the prize to move.
But although Monty’s action doesn’t causally change the prize’s location, it provides crucial probabilistic information by constraining which door he could open.
The lesson is quite simple: the way that we obtain information is no less important than the information itself.
As the causal diagram below shows, two things causally affect the “Door Opened” by Monty: (1) which door you pick; and (2) the location of the prize/car.
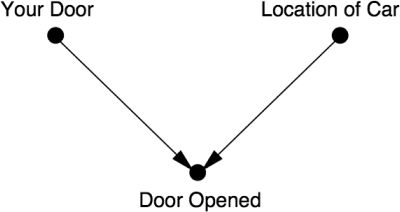
The diagram above shows a collider (see my summary of The Book of Why for more on colliders). Initially, “Your Door” and “Location of Car” are independent. However, they both causally determine which door Monty opens. So when you condition on a collider—i.e. once we know which door Monty opens—this creates a negative correlation between “Your Door” and “Location of Car” where none previously existed.
If you enjoyed this explanation, you may also like: